1、先考虑如下角格点三角形问题。
题目和图片放到一起。题目是以定理或命题的形式给出。

2、这个命题是比较容易证明的,下面就是这个命题的证明过程:

3、这个图形的等角共轭图形如下图所示,等角共轭图形实际上也是伴随图形:

4、保持∠A为9°和21°,还可以得到另外两个伴随图形:
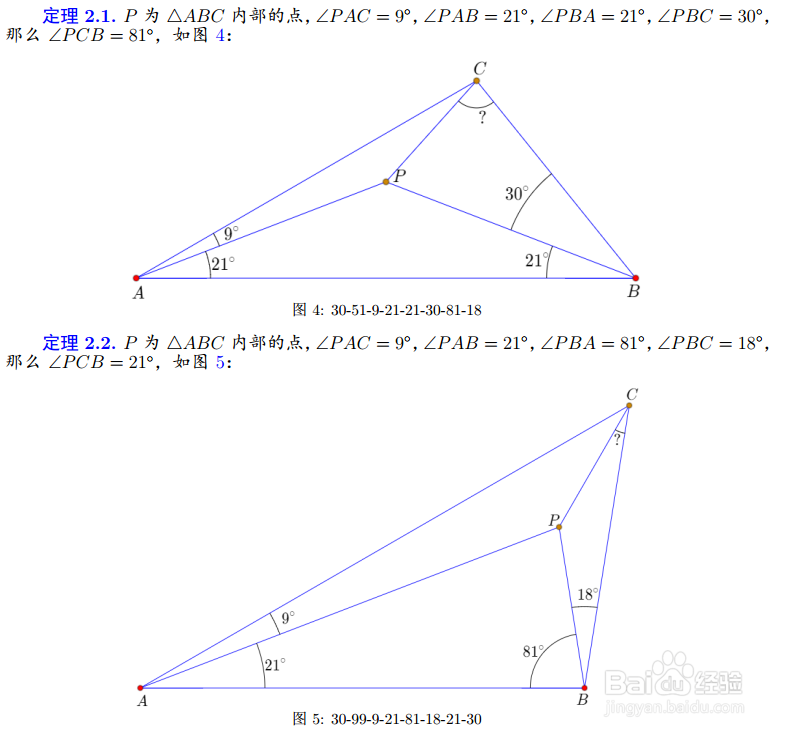
5、保持9°角在A点上端,把下端的21°角换为18°,则可以得到4个伴随图形:
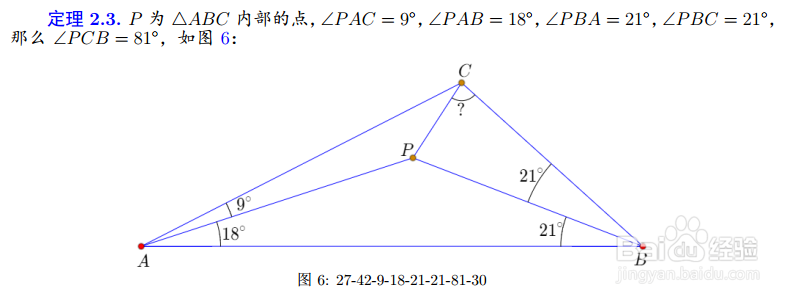
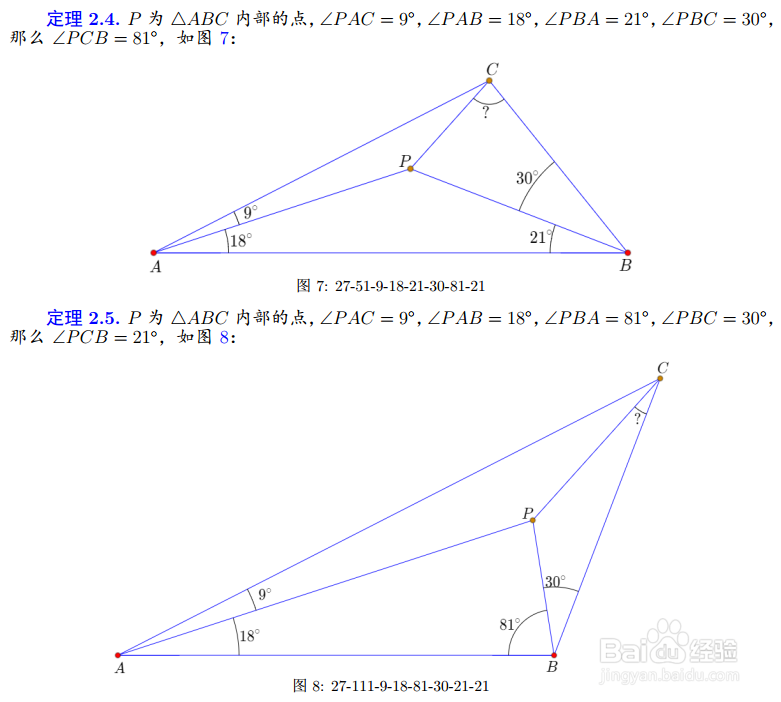
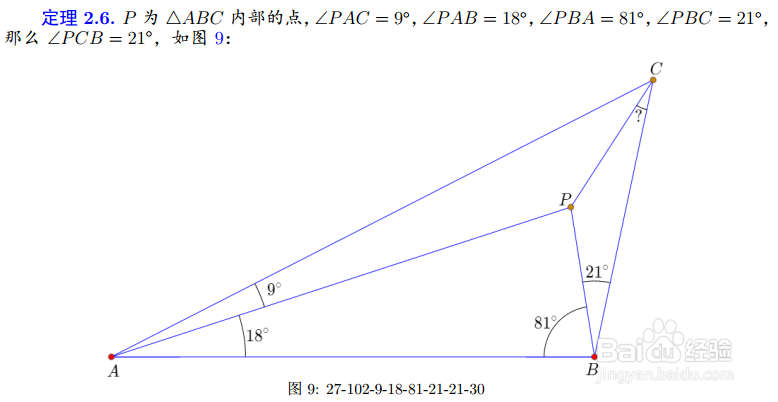
6、把18°替换为30°,还可以得到4个伴随图形:
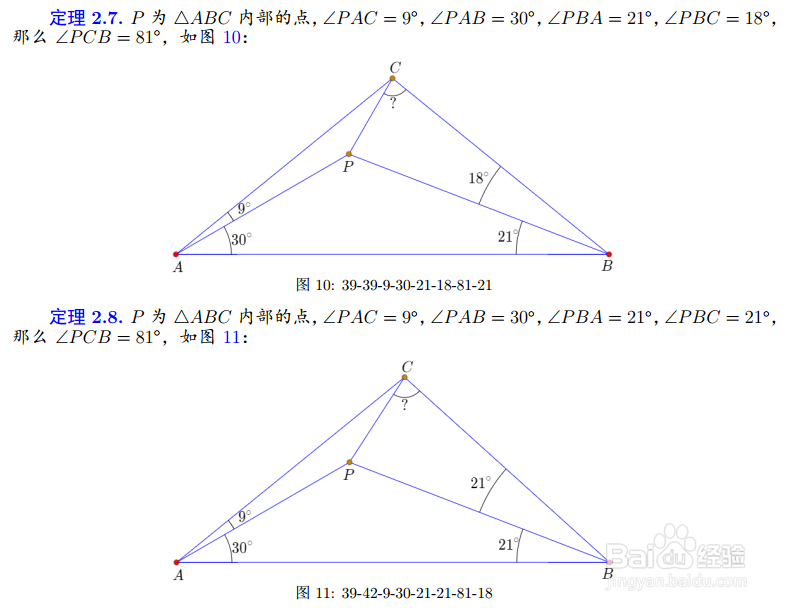
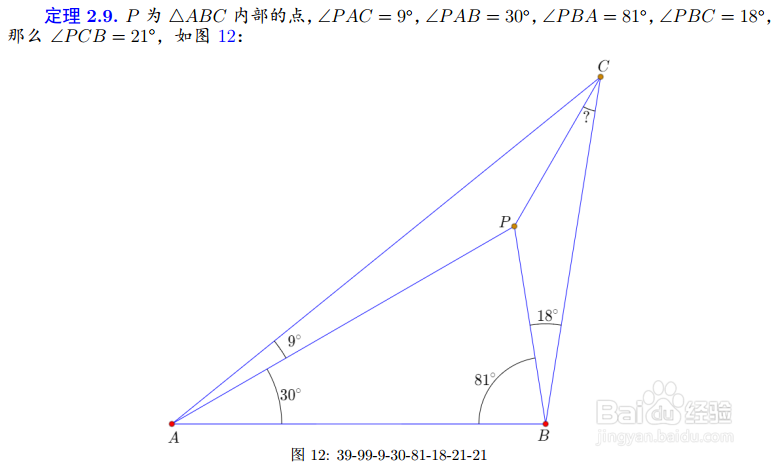
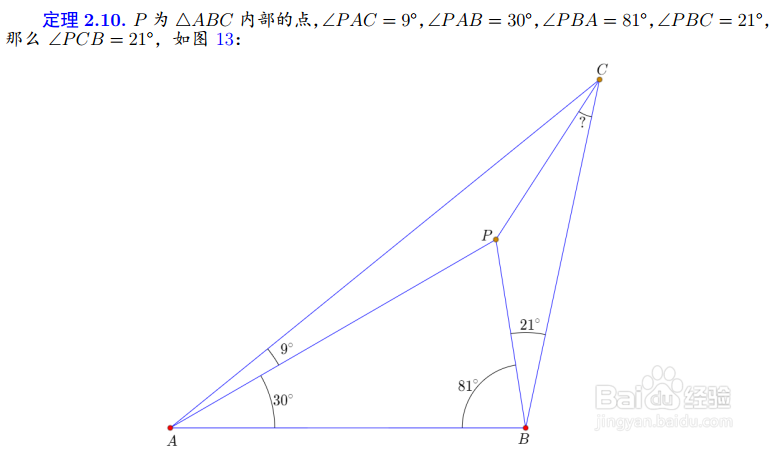
7、这样,算上原图形,就有了12个伴随图形。它们随着原图形的证明而得到统一证明。
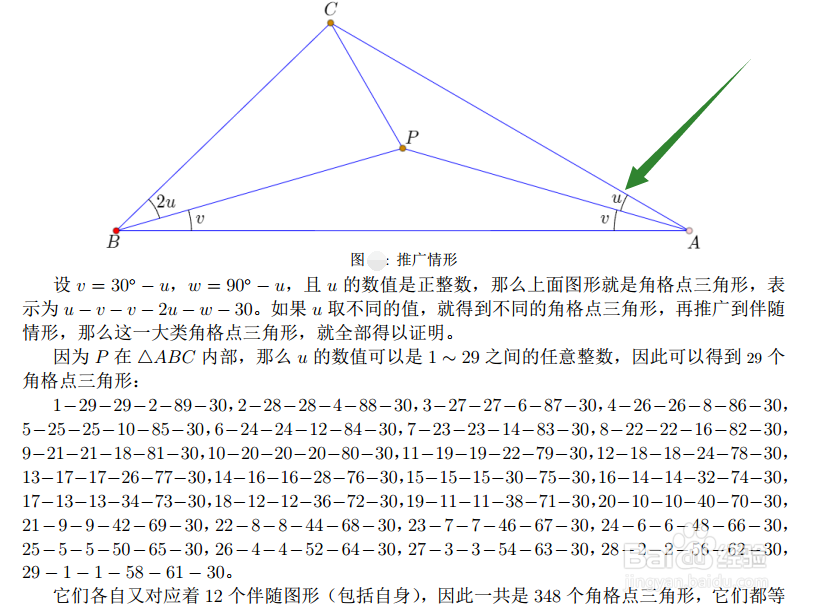
1、考虑如下的命题,读者请自行证明。
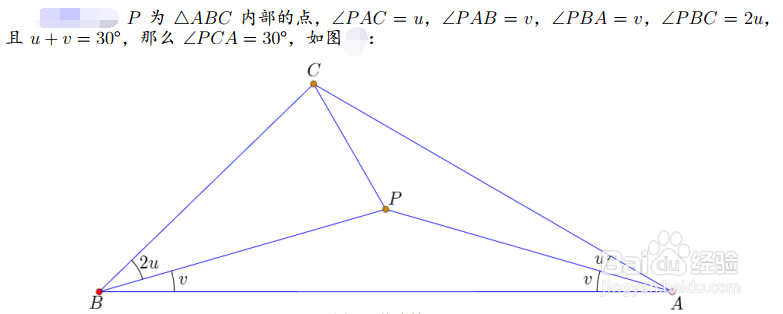
2、图中,u的度数数值可以是1到29之间的任意整数,再考虑各自的伴随图形,一共可以得到348个角格点三角形。