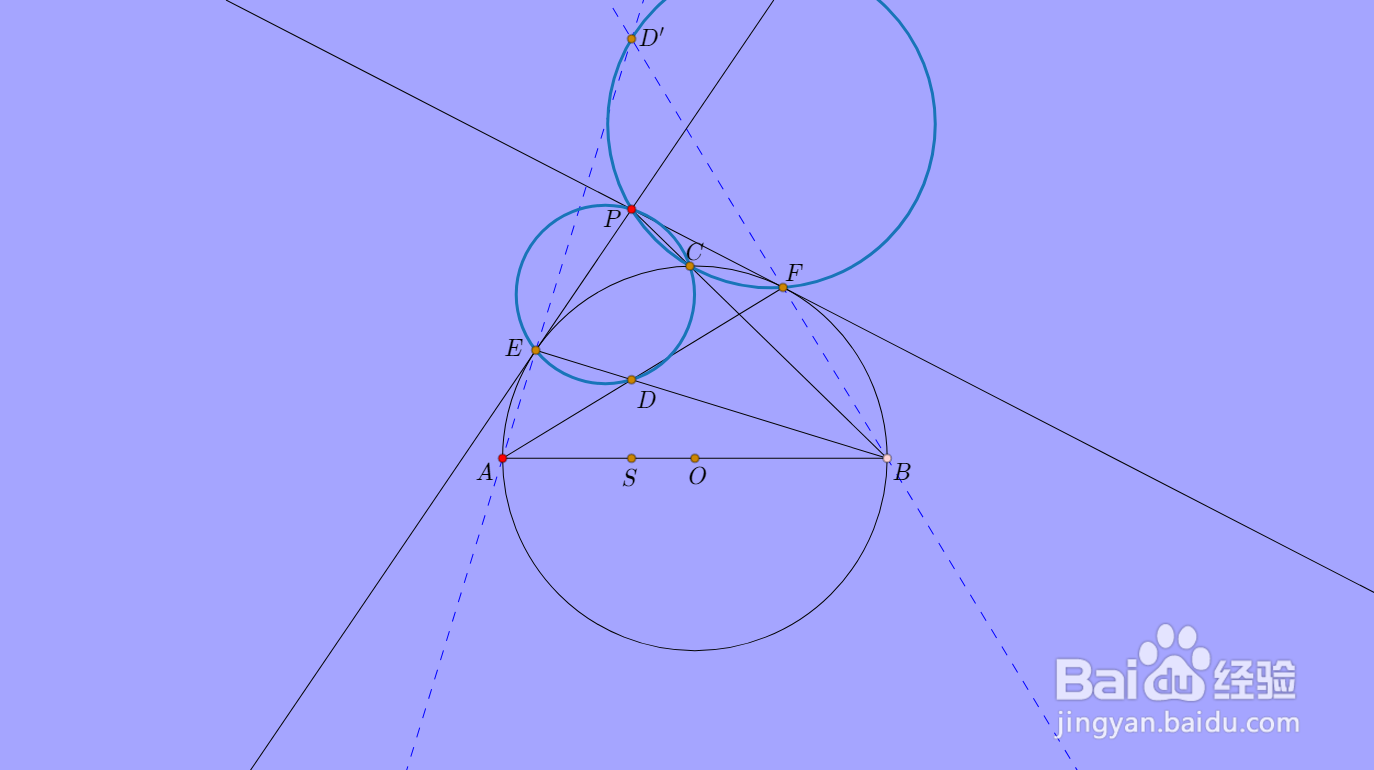
1、为了便于作图,用网络画板。
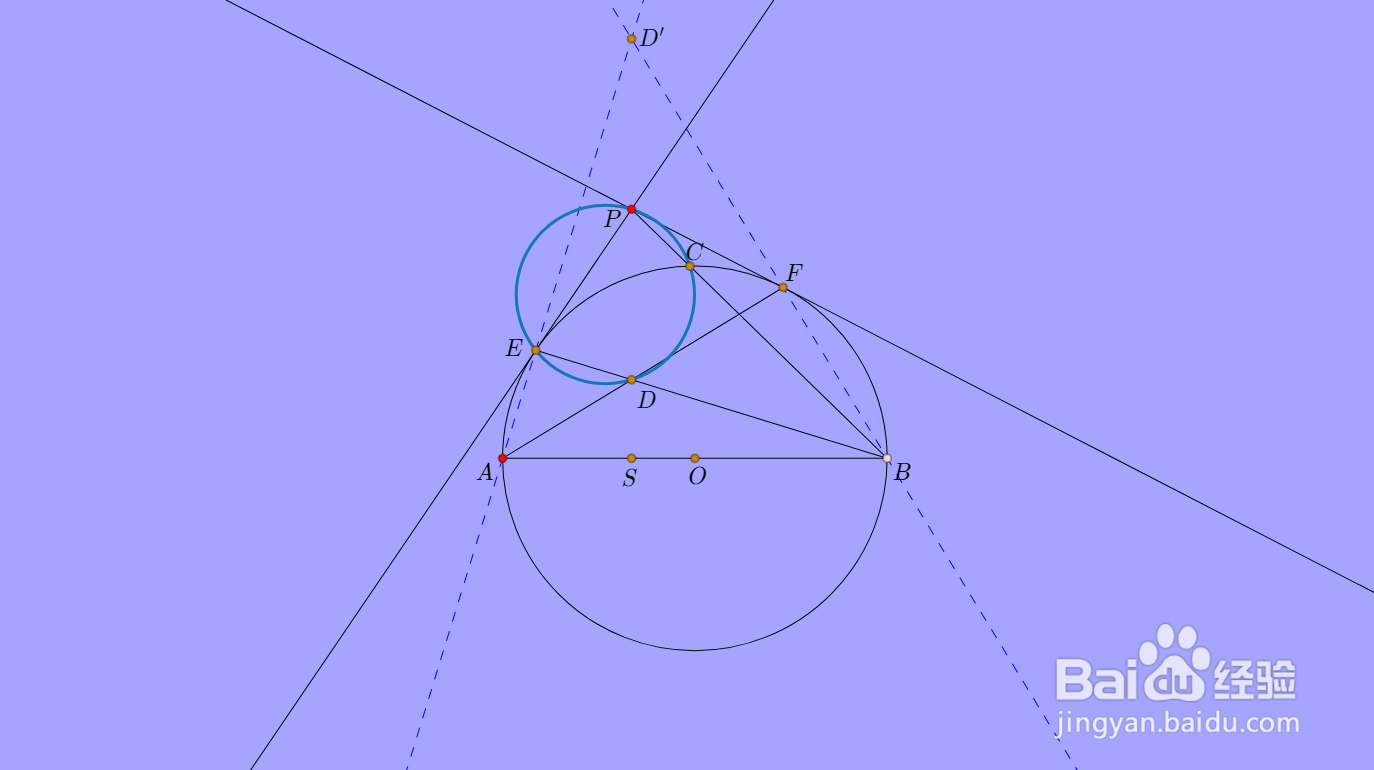
题图如下:
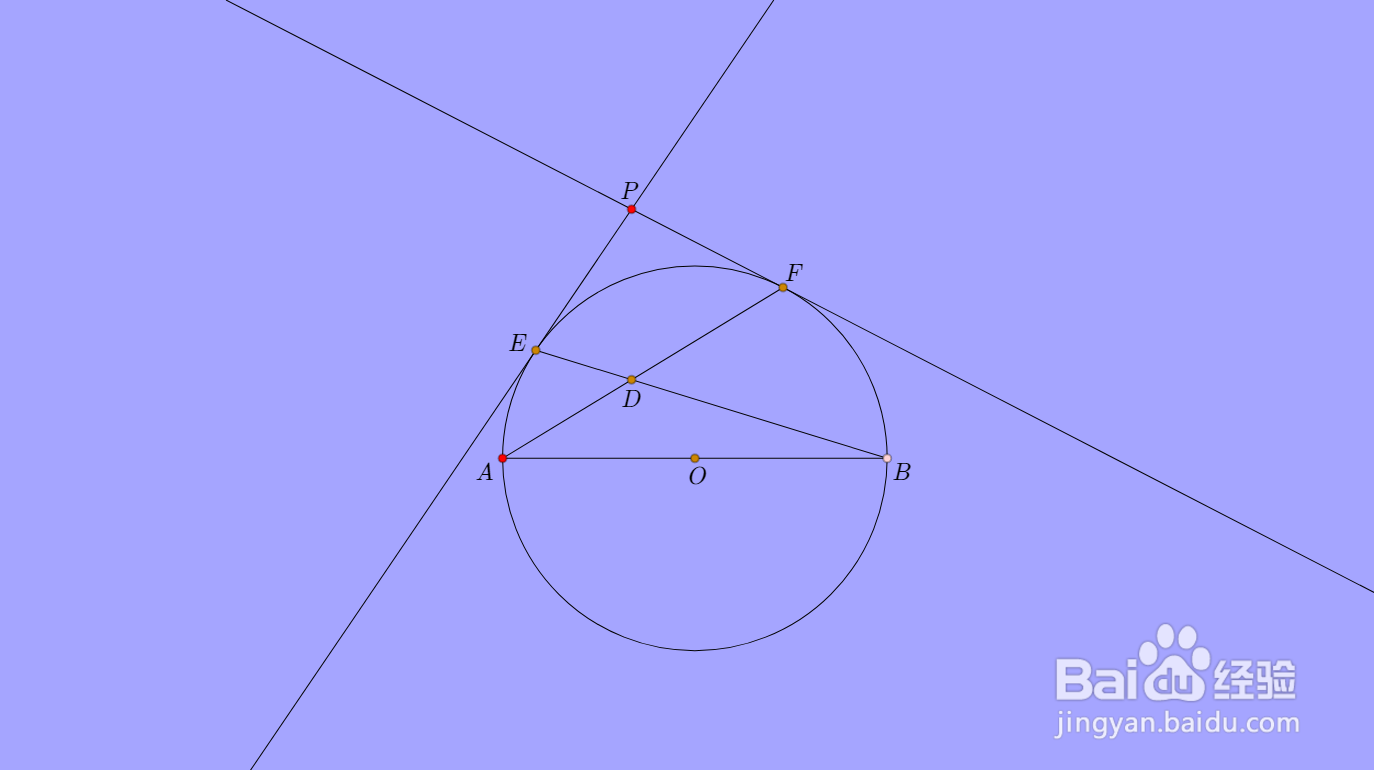
2、设直线AE和BF交于D',那么容易发现D是三角形ABD'的垂心。
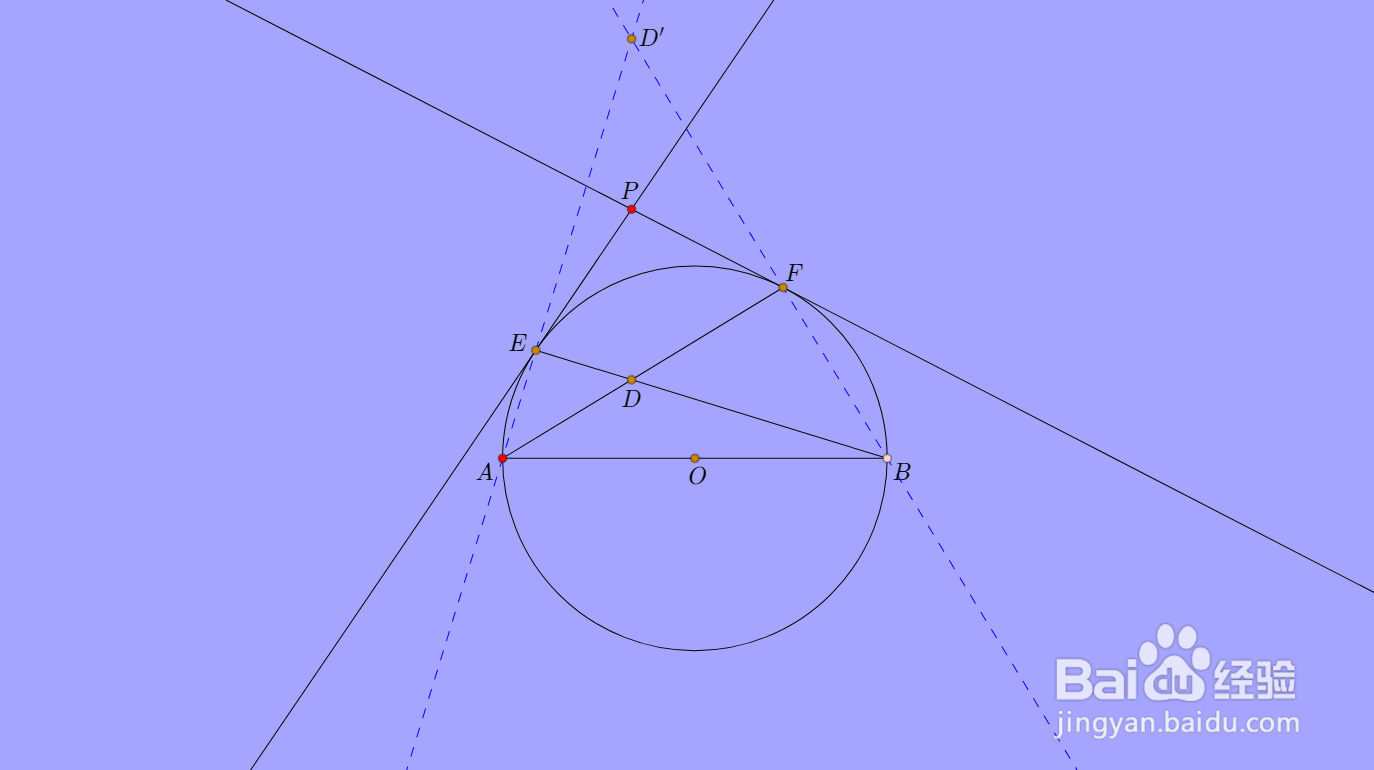
3、考虑D关于圆O的极线,是什么。
D的极线必定经过D'点,另一个点则是AB和EF的交点U。
那么直线UD'就是D的极线。
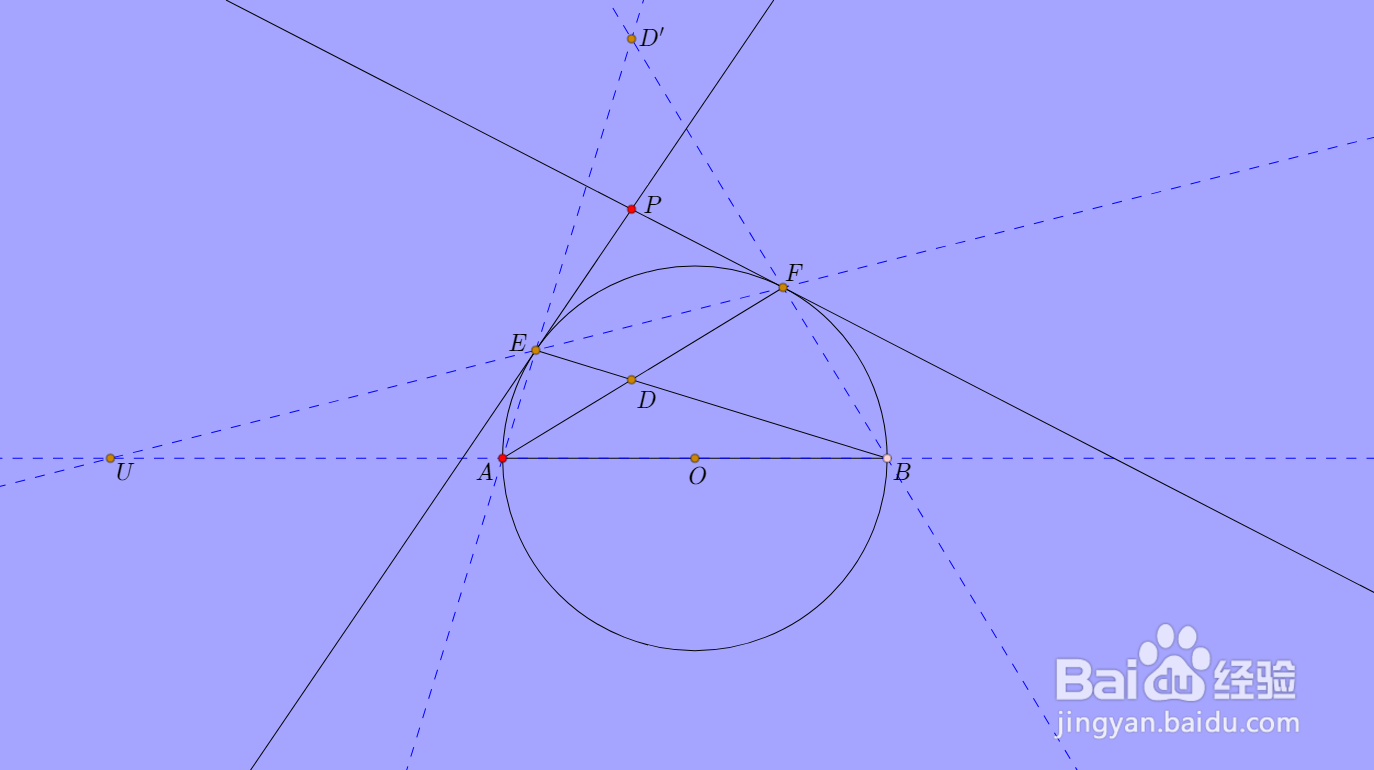
4、UDD'实际上是自极三点形:
D的极线,是直线UD';
D'的极线,是直线UD;
U的极线,是直线DD'。
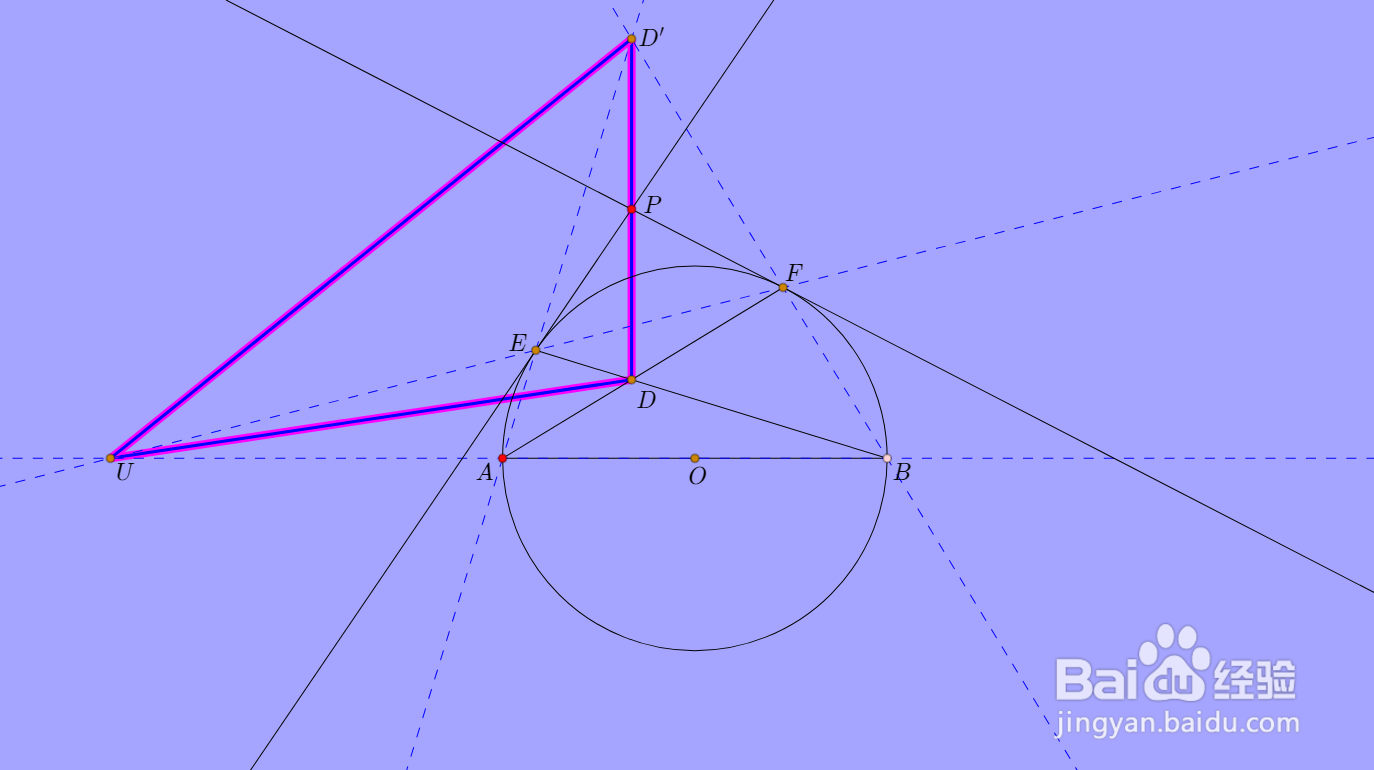
5、U、E、F三点共线,它们的极线也得共点,即DD'、PE、PF三线共点,这个点就是点P。
也就是说,DD'P共线。
进而说明,PD垂直于AB。
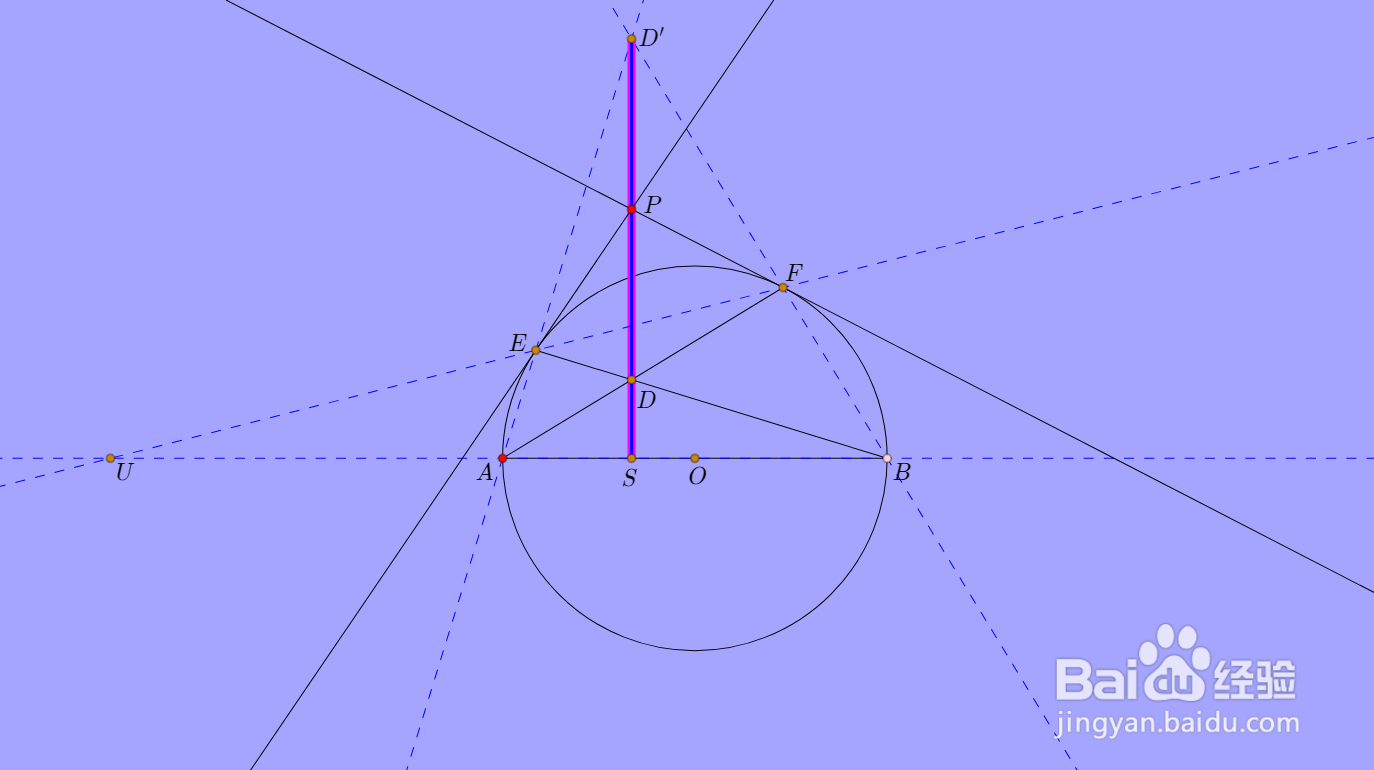
6、垂足记为点S,则:
∠PDF=∠ADS=∠ABF=∠AFP,所以PD=PF。
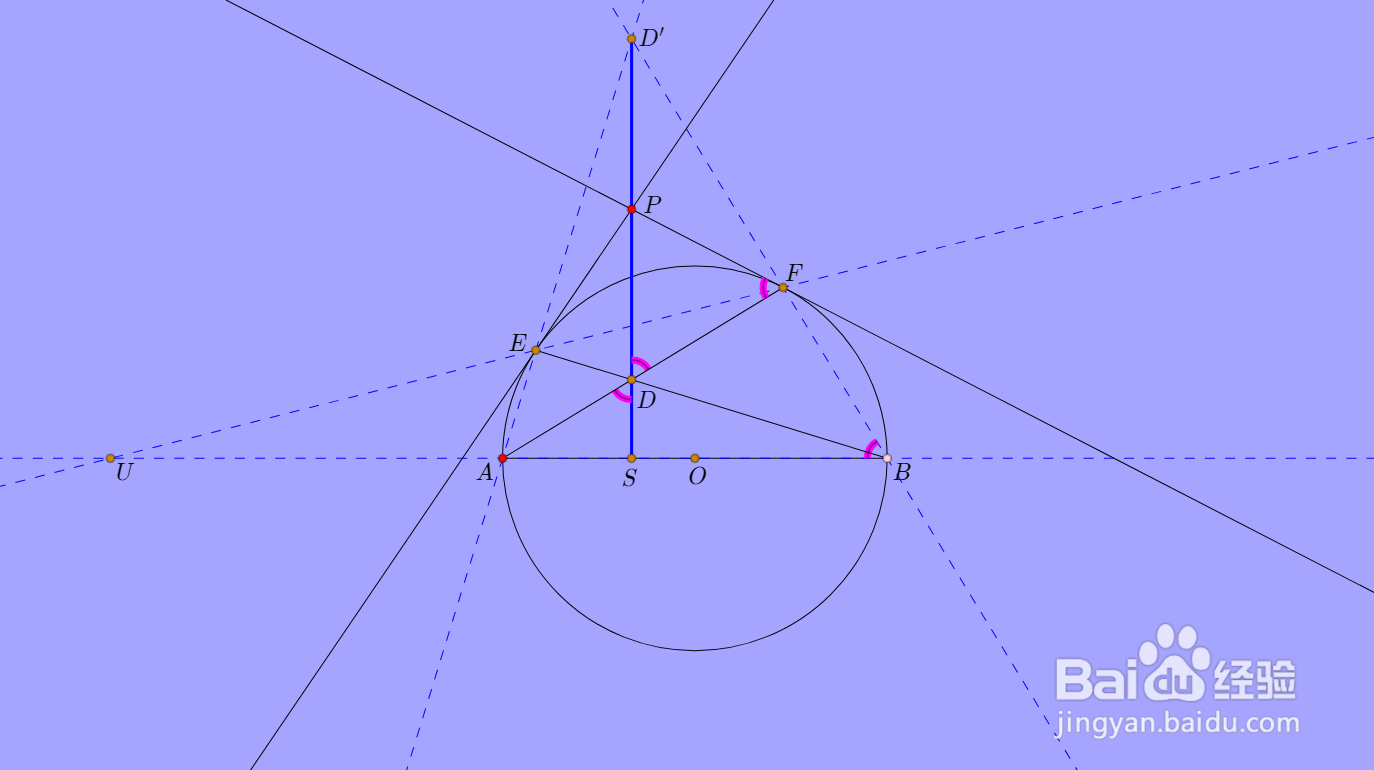
7、这样就证明了PD=PE=PF的结论。
实际上,P是线段DD'的中点。
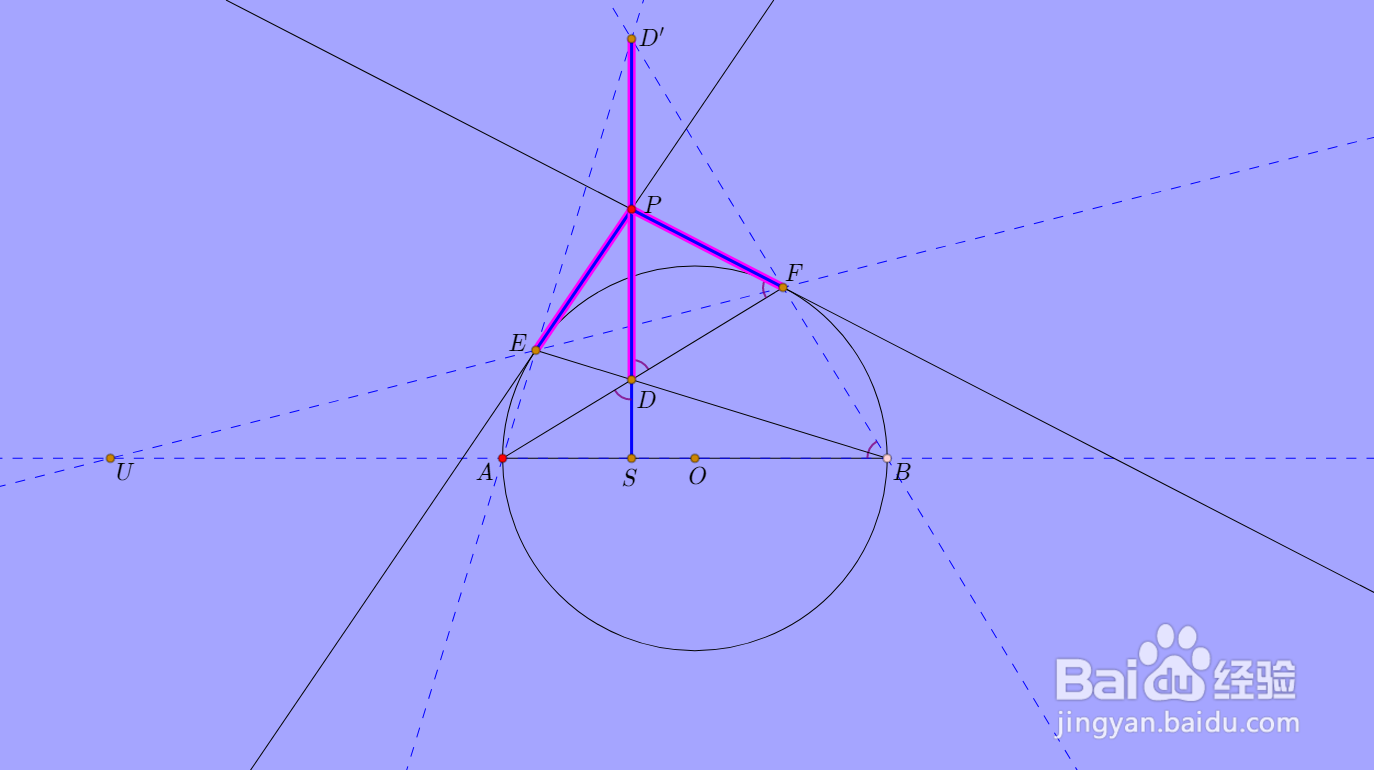
8、还可以进一步证明,PCDE四点共圆。
9、类似的,还有PCFD'四点共圆。