1、基于动态规划思想,构建算法,步骤如下:
1. 创建一个长度为 n 的数组 dp,用于存储 1 到 n 阶台阶的所有爬楼梯方式;
2. 对于 i 阶台阶,因为每次只能迈 1 或 2 级台阶,所以其方式是:爬到第 i-1 阶再爬 1 阶,或者爬到第 i-2 阶再爬 2 阶,即 dp[i] = dp[i-1] + dp[i-2]。

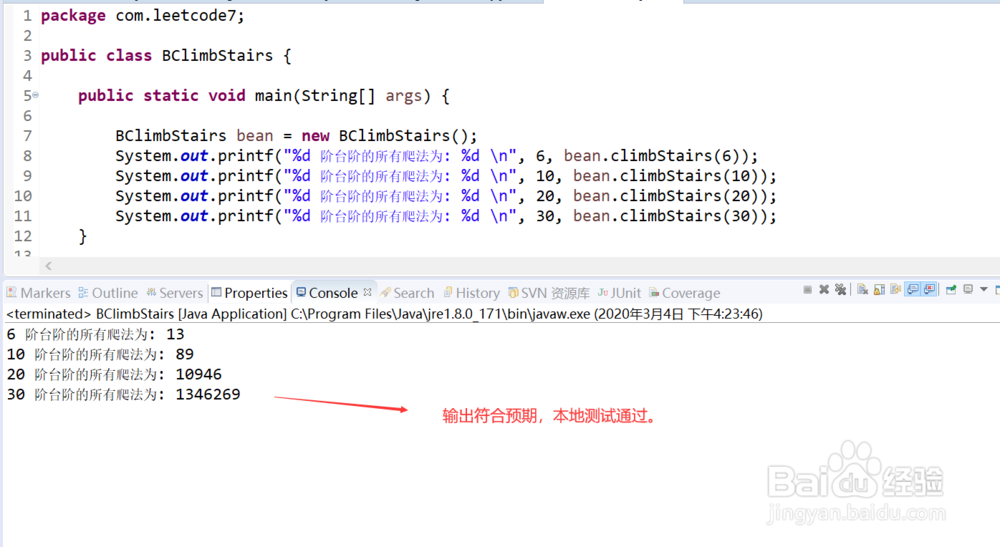
2、编写本地测试主方法。

3、运行本地测试主方法,观察控制台输出,符合预期,本地测试通过。
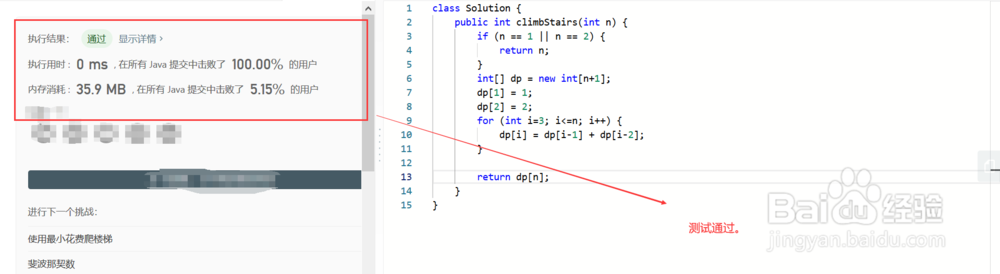
4、平台提交算法,测试通过。
5、算法复杂度分析:算法需要遍历 1 到 n 所有数字,因此时间复杂度为 O(n) ;需要创建长度为 n 的数组用于存储中间计算结果,因此空间复杂度也为 O(n) 。
