1、 函数的定义域,本题是一次函数的绝对值,根据函数特征,自变量x可以取全体实数。
y = 2 x + 1 + x + 4
根据函数的特征,自变量x可以取全体实数。
则函数的定义域为:
( - ∞ , + ∞ )

2、绝对值涉及到的零点;
1.当2x+1=0时,则:
零点x1=-1/2;
2.当x+4=0时,则:
零点x2=-4。

3、按照绝对值涉及的零点,去绝对值并解析函数的表达式。

4、1.当x∈(-∞,-4)时,
y=-2x-1-x-4
=-3x-5;
2.当x∈[-4,-1/2]时,
y=-2x-1+x+4
=-x+3
3.当x∈(-1/2,+∞)时,
y=2x+1+x+4
=3x+5。
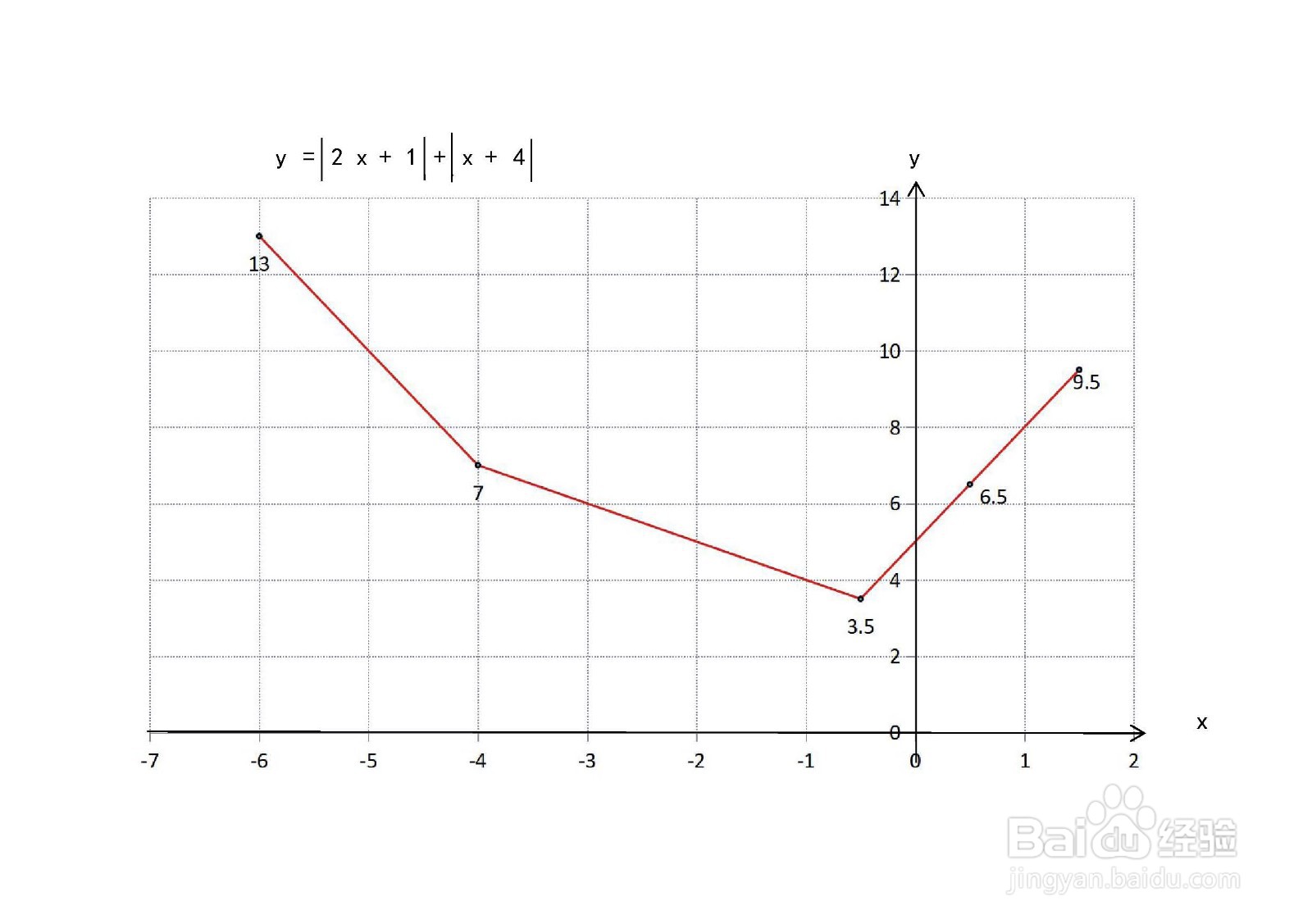
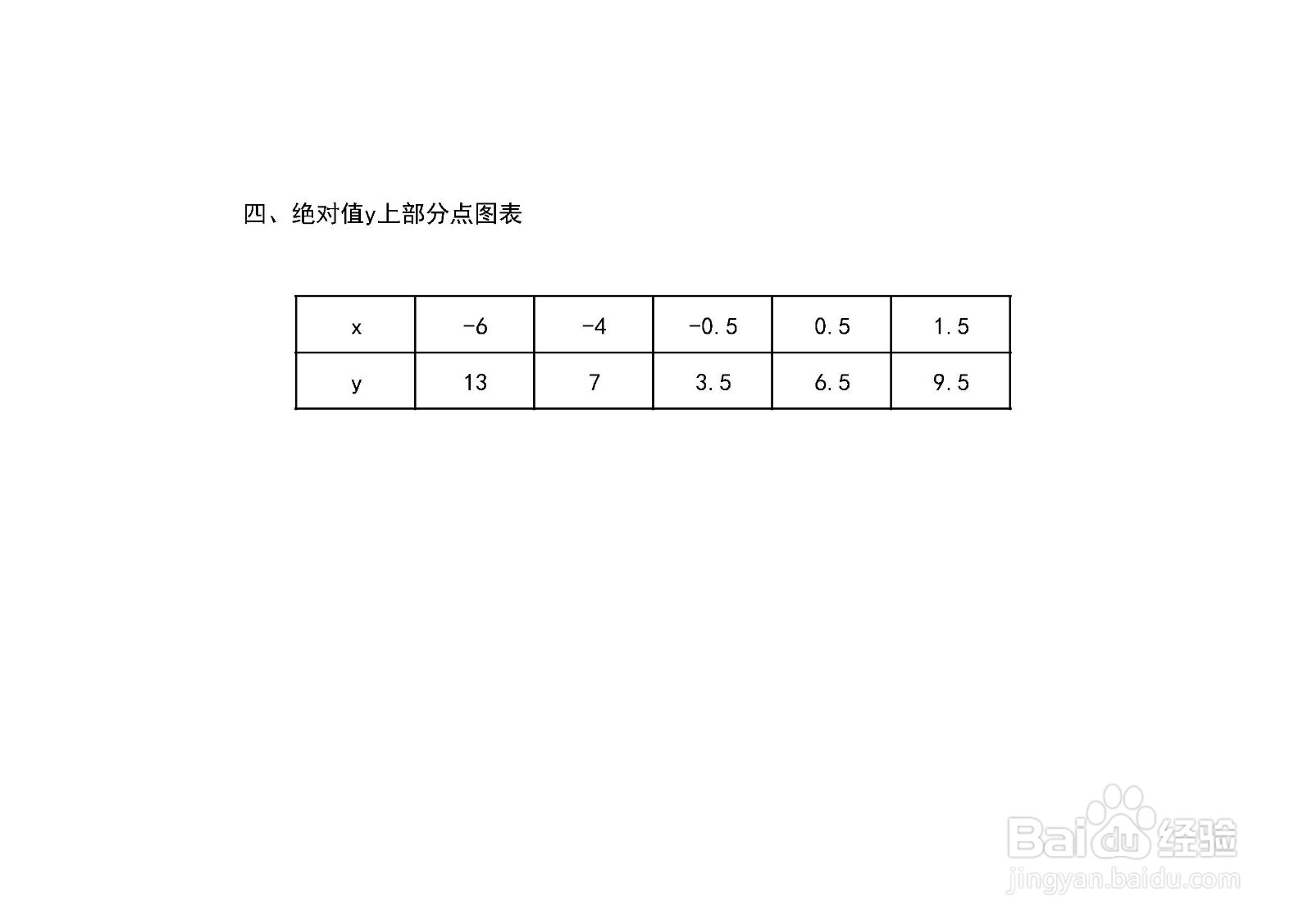
5、绝对值的五点图。
6、综合上述情况,绝对值图像示意图如下: