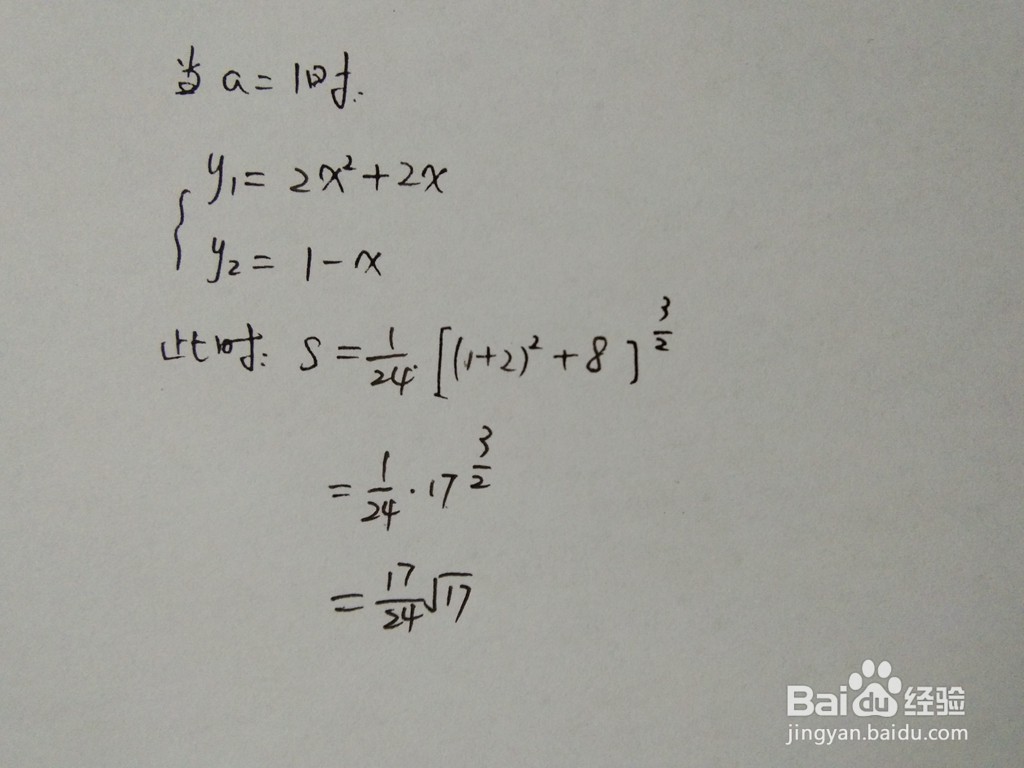1、联立抛物线y1和直线y2建立方程,将直线y2代入到抛物线方程y1中,得到x的一元二次方程,利用求根公式求交点通式如下:
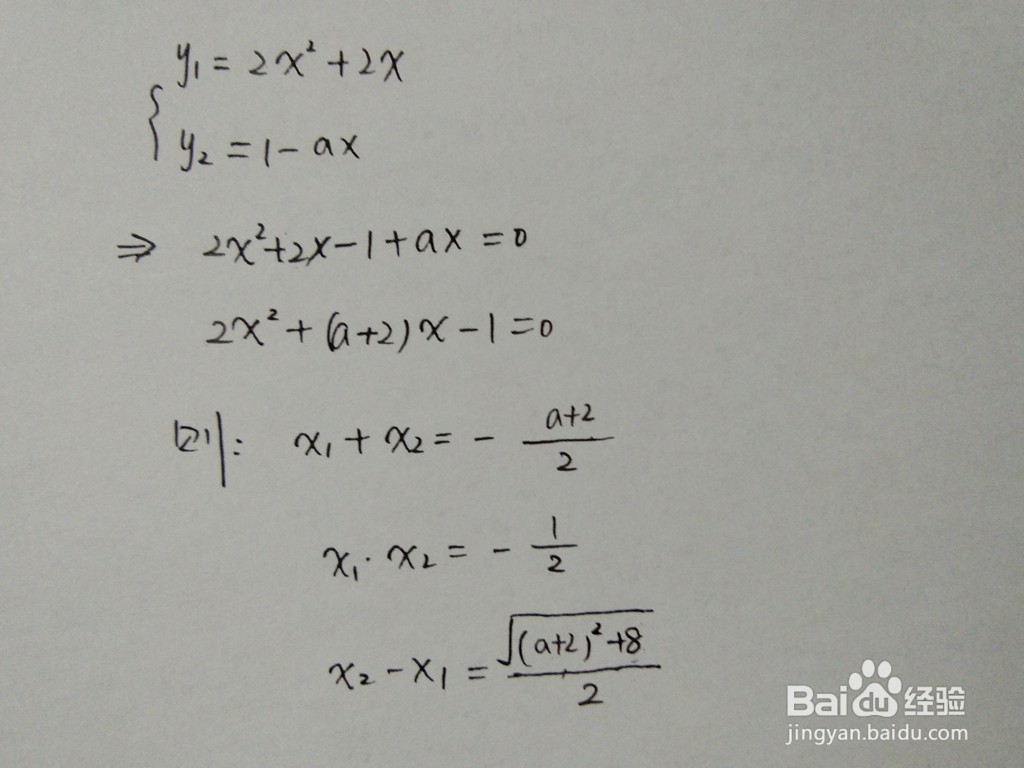
2、通过定积分求曲线区域面积计算规则,求出抛物线y1与直线y2围成面积通式如下:
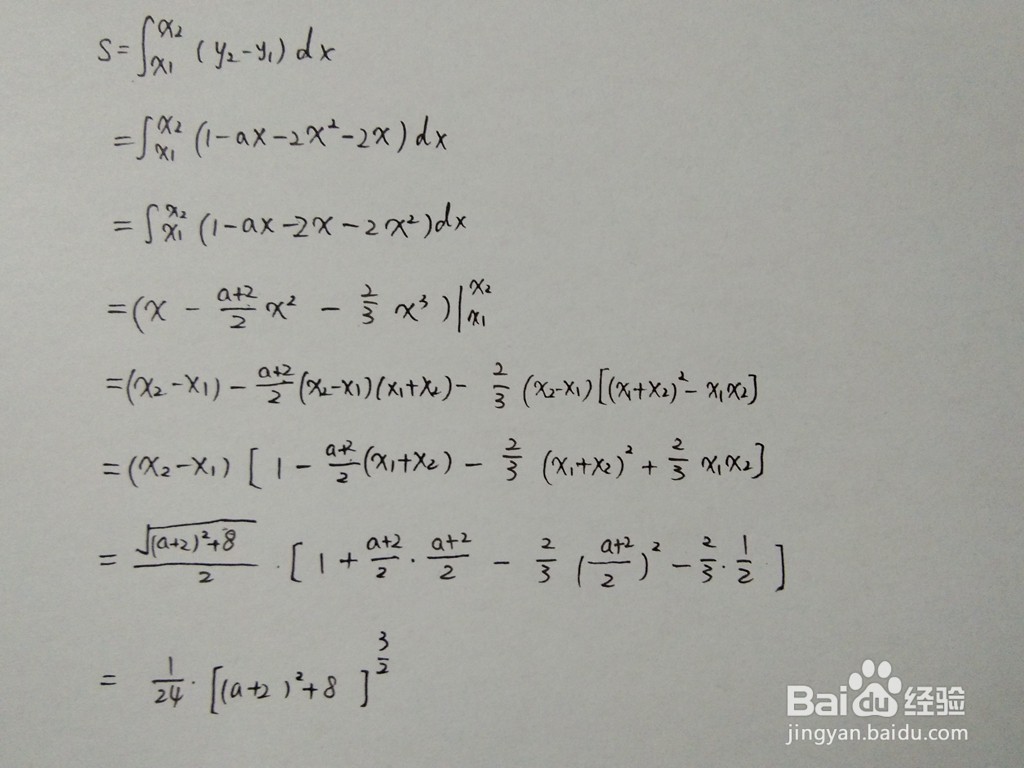
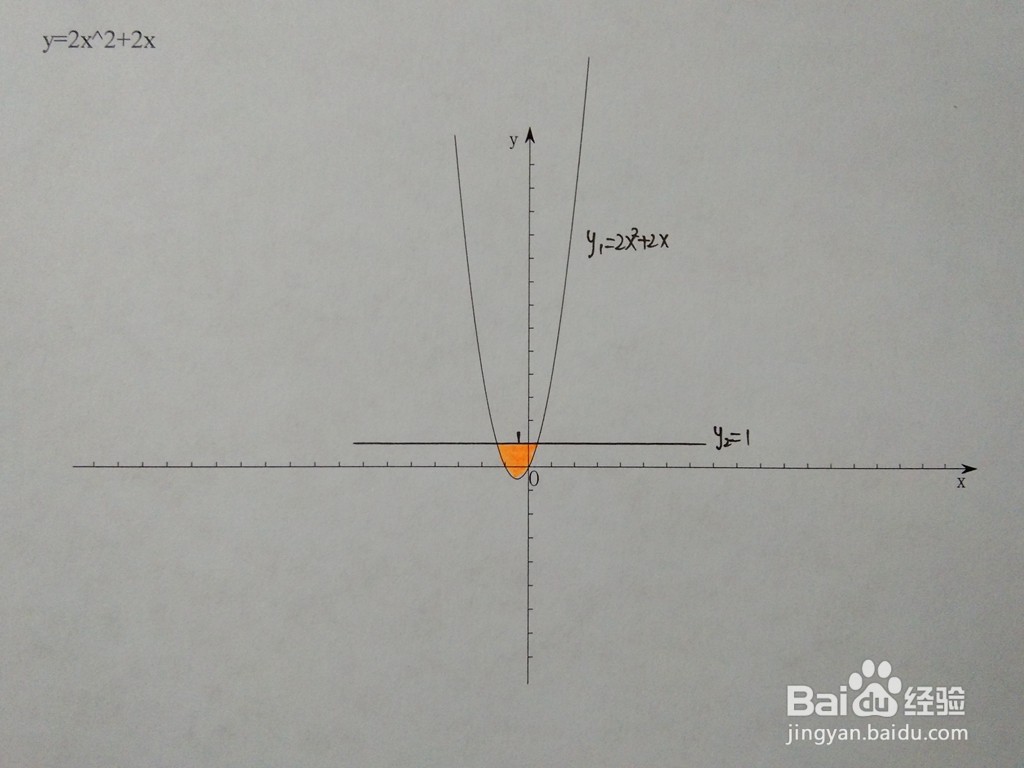
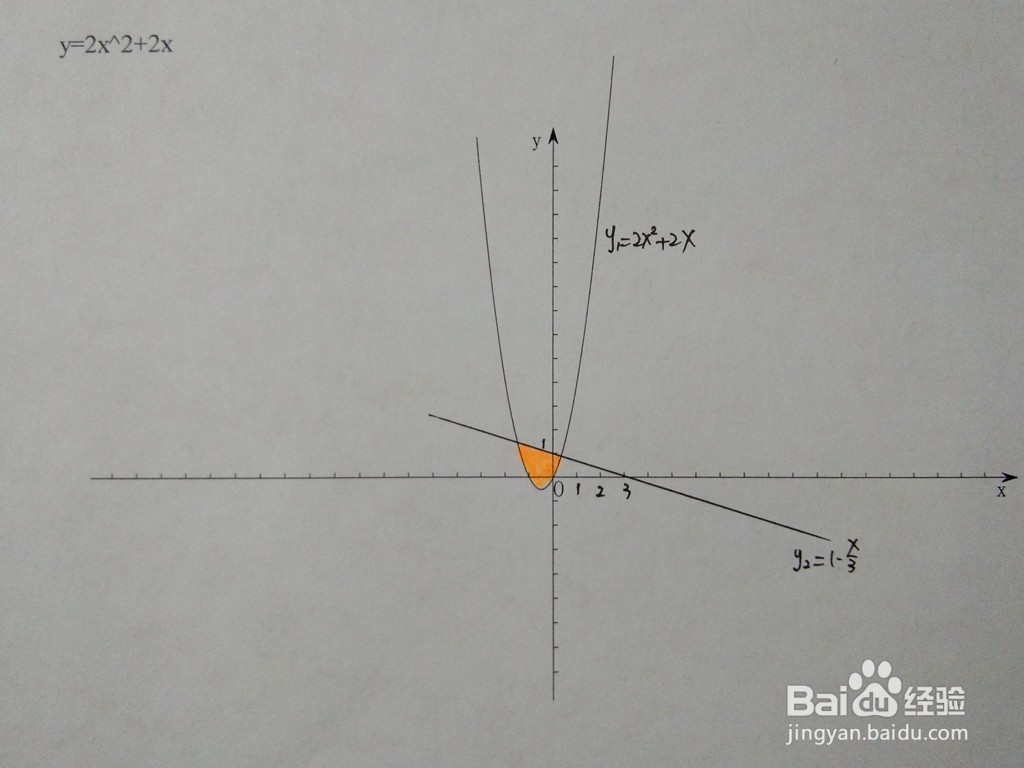
1、此时y2为平行于x轴的直线,曲线和直线的直角坐标系示意图如下所示。
2、根据面积通式,可求出此时直线与曲线围成的面积结果。
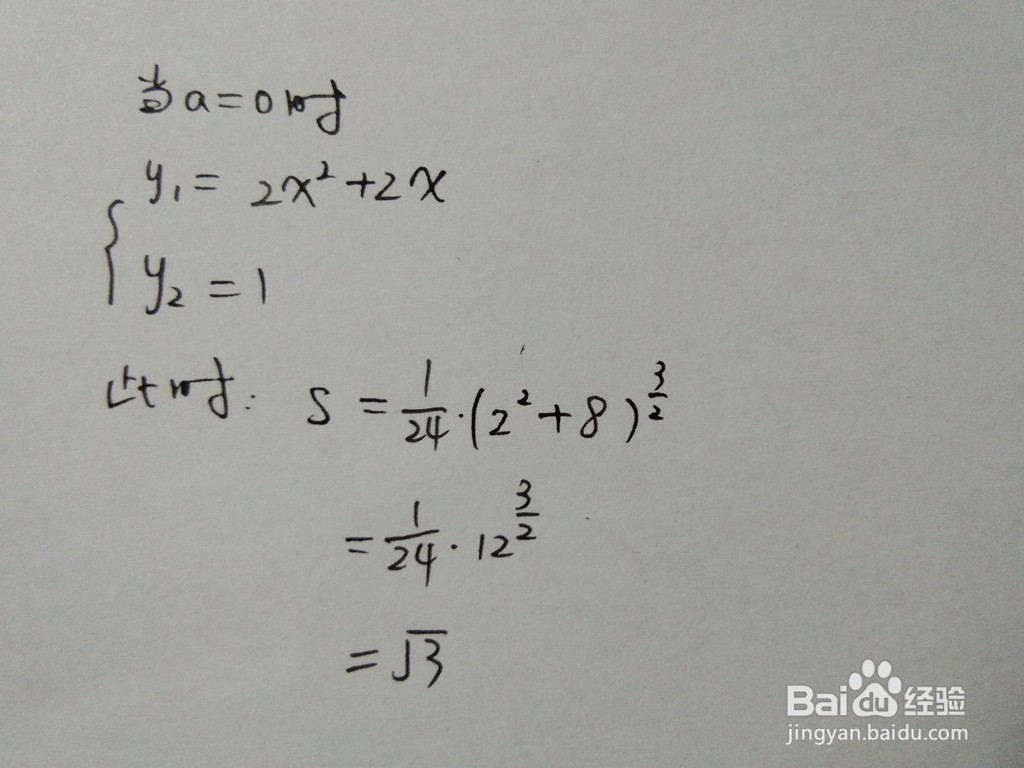
1、此时y2=1-x/3,曲线y1和直线y2在同一个直角坐标系示意图如下所示。
2、根据面积通式,可求出此时直线与曲线围成的面积结果。
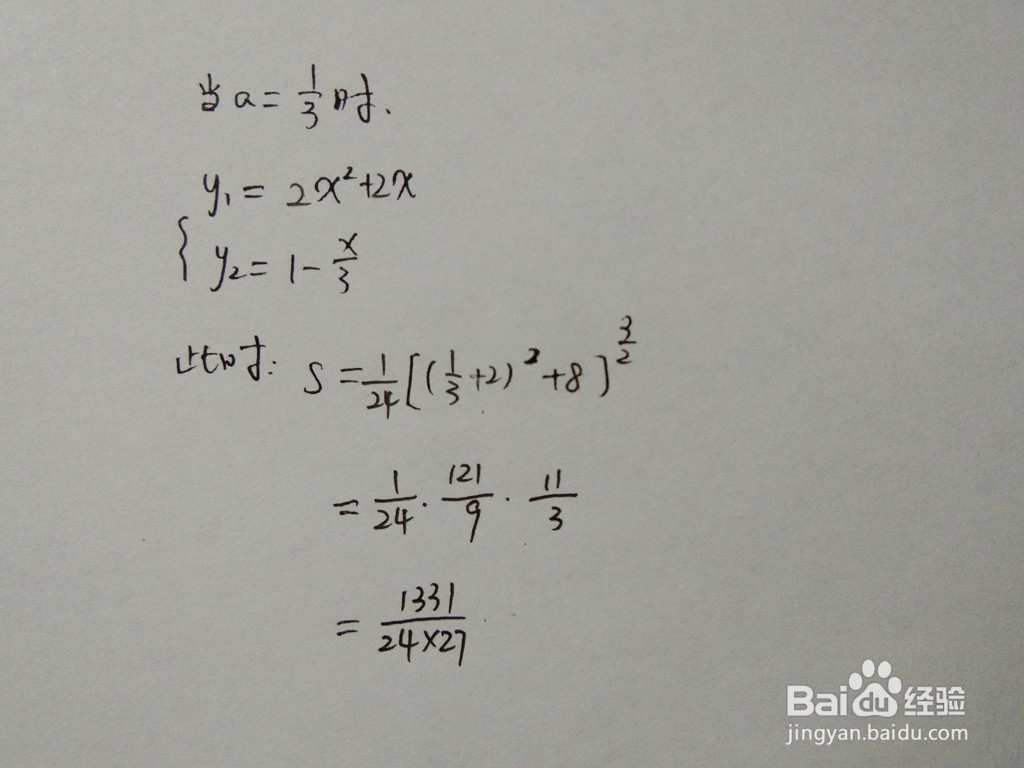
1、此时y2=1-x/2,曲线y1和直线y2在同一个直角坐标系示意图如下所示。
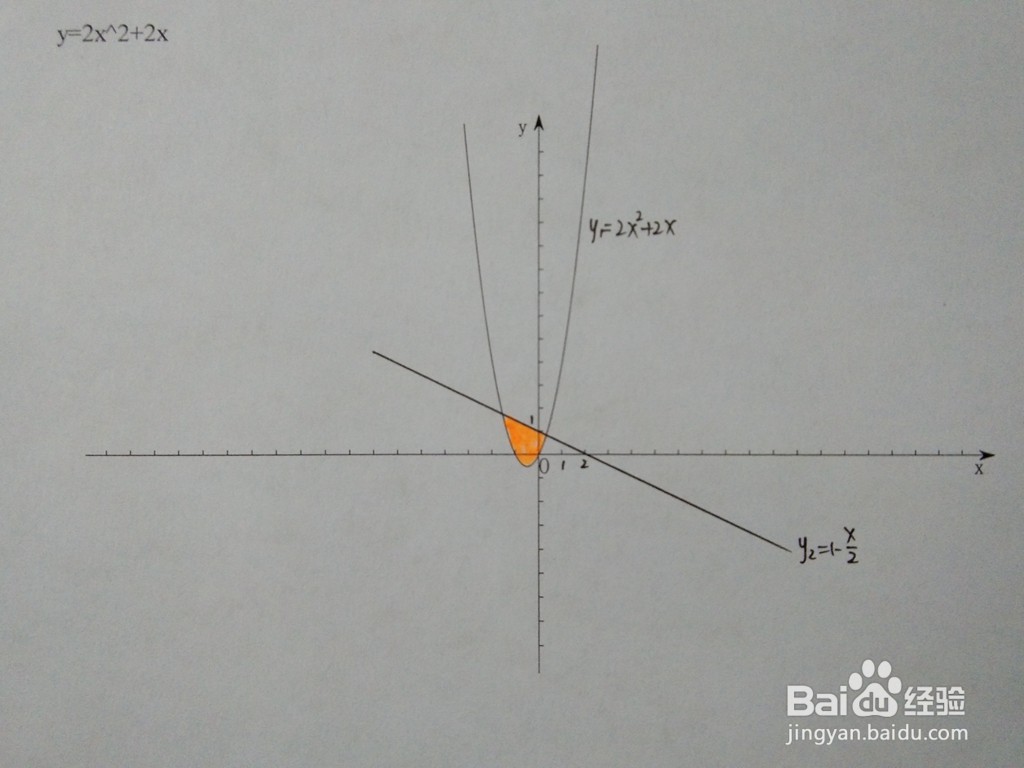
2、根据面积通式,可求出此时直线与曲线围成的面积结果。
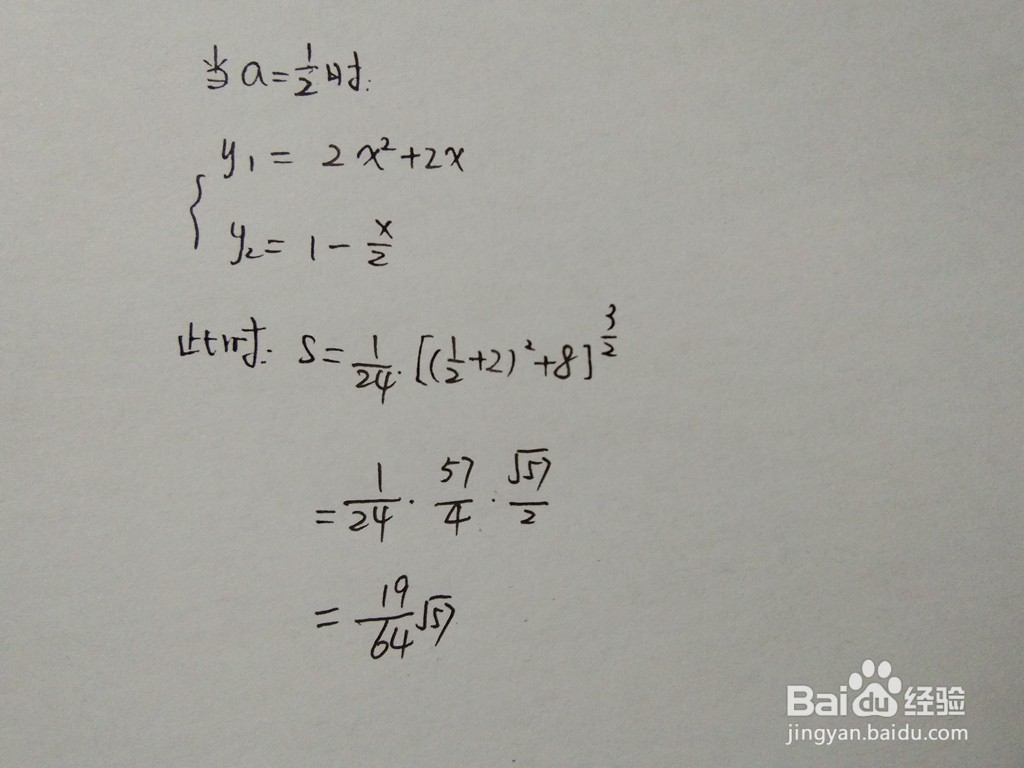
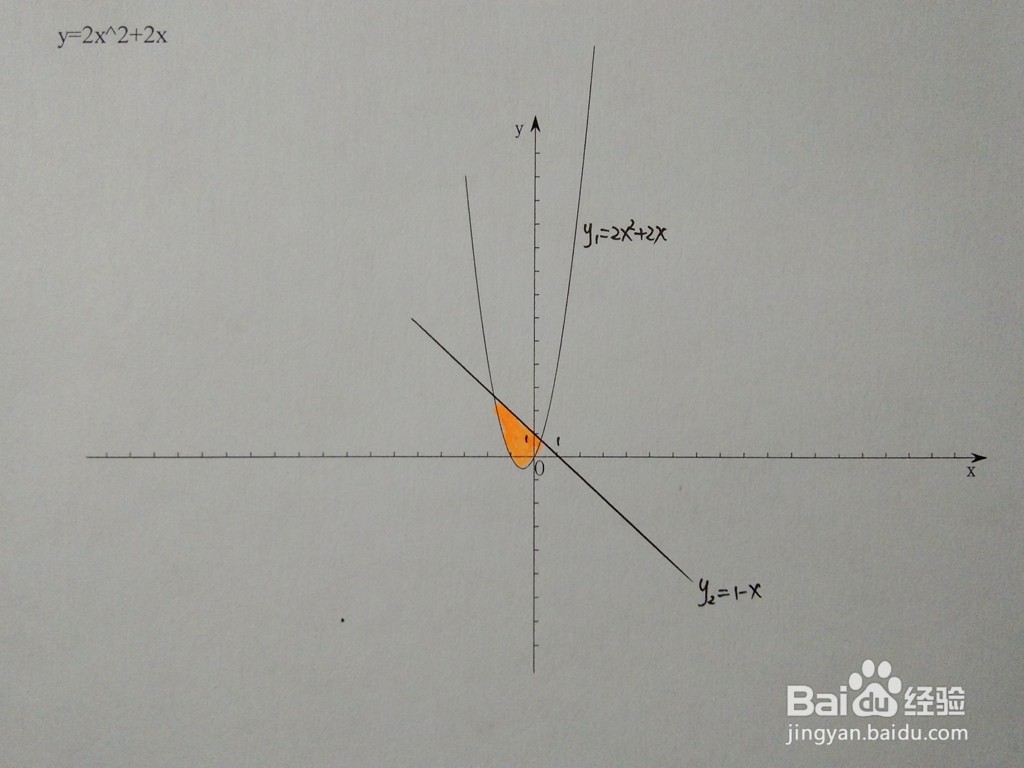
1、此时y2=1-x,曲线y1和直线y2在同一个直角坐标系示意图如下所示。
2、根据面积通式,可求出此时直线与曲线围成的面积结果。